宇宙の終焉を告げる？エントロピー増大の法則 – 時間の矢からブラックホールまで

「なぜ、美しく整えたはずの部屋は、放っておくと必ず散らかるのだろう？」

「なぜ、コーヒーにこぼしたミルクは、二度と元の美しい白い滴には戻らないのだろう？」

「そして、なぜ私たちの『時間』は、過去には決して戻らず、未来へと一方的に進むのだろう？」

こうした日常の素朴な疑問は、私自身が宇宙の仕組みに魅了されるようになった原点です。そして驚くべきことに、これらの答えはすべて、宇宙を貫くたった一つの絶対的な法則、「エントロピー増大の法則（熱力学第二法則）」に繋がっています。

これは単なる物理学の解説ではありません。私たちがなぜ「過去」を記憶し、「未来」を夢見ることができるのか、その根源に触れる知の旅です。私自身の探求の物語と共に、あなたの世界観を根底からアップデートする旅にご案内します。

第1章：エントロピーとは何か？ – 宇宙の「ありふれた状態」を目指す流れ

エントロピーはよく「乱雑さの度合い」と説明されます。間違いではありませんが、私自身、この言葉だけでは本質を掴みきれませんでした。その本当の意味は、より深く、そしてシンプルです。

物理学の世界では、エントロピーは「その状態を取りうる、微視的な場合の数」で定義されます。この概念を美しい数式で表現したのが、オーストリアの物理学者ルートヴィッヒ・ボルツマン。彼はその功績を、自身の墓石にこの式を刻むことで永遠のものとしました。

• S: エントロピー
• k: ボルツマン定数（物理学の基本的な定数）
• W: その状態を取りうる「場合の数」

私がこの式に出会った時、最初は難解に感じましたが、そのメッセージは驚くほど明快でした。「場合の数が多い、ありふれた状態ほどエントロピーが高い」。ただ、それだけなのです。

では、この「場合の数」とは何でしょうか？ 新品のトランプで考えてみましょう。カードは数字の順に完璧に並んでいます。この「整然とした状態」は、厳密にはたった1通りしかありません。つまり「W」が極端に小さく、エントロピーは非常に低い状態です。しかし、一度シャッフルすればどうでしょう？ カードの並び順の組み合わせ（場合の数）は「52の階乗（52!）」、これは8の後ろに0が67個も続く天文学的な数になります。この、ごちゃごちゃで「ありふれた状態」こそが、高エントロピー状態なのです。

重要なのは、シャッフルしたトランプが偶然にもう一度元の完璧な順番に戻ることが確率的にあり得ないように、物事はより確率の高い（場合の数が多い）状態へ自然と移っていく、ということ。部屋が散らかるのも、コーヒーにミルクが混ざるのも、全て同じ原理。「整った状態」よりも「散らかった状態」のほうが、実現されうる「場合の数」が圧倒的に多い。宇宙は、ただ確率に従って、最も「ありふれた」状態へと向かっているだけなのです。

そして、この元に戻れないという絶対的なルールこそが、なぜ私たちが過去を思い出し、未来を夢見ることができるのか、という「時間」そのものの本質を規定しているのです。第2章では、宇宙の始まりにまで遡り、この壮大な謎に挑みましょう。

第2章：「時間の矢」はなぜ未来にしか向かわないのか？ – 宇宙の初期設定の謎

物理法則の多くは、実は「時間対称」です。ボールを投げる映像を逆再生しても、物理的には何ら不自然ではありません。しかし、現実の私たちは過去に戻ることはできず、時間は未来に向かって一方的に流れていきます。この「元に戻れない」性質を「時間の矢」と呼びます。

では、なぜ時間の矢は常に未来を指すのか？ その向きを絶対的に決定づけているのが、エントロピー増大の法則なのです。

その壮大な物語は、138億年前に遡ります。宇宙の始まりであるビッグバンが、極めて特殊で奇跡的な「超・低エントロピー状態」だったからです。これこそが、全ての原因の「最初の原因」と言えます。

初期の宇宙は非常に高温・高密度で、ほぼ完璧に均一でした。これを知った時、私自身、最初は混乱しました。「均一なら、ごちゃごちゃで高エントロピーなのでは？」と。しかし、重力が支配する宇宙では、私たちの直感は全く逆になります。

重力がない部屋では、気体が均一に広がるのが最も「ありふれた」高エントロピー状態です。しかし、物質を互いに引き寄せ一点に集めようとする重力がある宇宙では、物質が均一に散らばっている状態は、まるで無数の鉛筆の先端をすべて下にして完璧に立たせるような、極めて「ありえない」、つまり「場合の数が少ない」特殊な状態（低エントロピー）なのです。そこから重力で集まって星や銀河といった構造ができる方が、遥かに自然で「ありふれた」状態（高エントロピー）と言えます。この重力が直感を裏切る点こそ、初心者がつまずきやすいポイントであり、宇宙のエントロピーを理解する鍵なのです。

つまり、私たちが「未来」と呼んでいるものは、宇宙全体が、ありえないほど特殊だった初期状態から、よりありふれた状態へと移り変わっていく方向そのものなのです。この宇宙の初期設定が、「原因と結果」という関係を生み、記憶は過去のものであり、希望は未来のものであるという、私たちの意識の根幹すら規定しているのかもしれません。

生命という秩序すら、宇宙全体のエントロピー増大という大きな流れの一部でした。では、この法則が試される究極の場所、光さえも脱出不可能な「ブラックホール」ではどうなるのでしょうか？ 法則が破られるのか、それとも我々の想像を超える形で君臨し続けるのか。宇宙で最も過酷な論争の最前線へ向かいます。

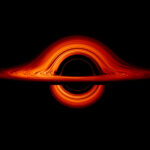
第3章：ブラックホール – 宇宙最大のエントロピー製造機か、法則の破壊者か

宇宙のあらゆる活動は、エントロピーを増大させるプロセスの一部です。その中でも王様と呼べる存在が、宇宙で最もシンプルかつ究極の天体、ブラックホールです。

一見すると、ブラックホールはエントロピーの法則にとって「天敵」のように思えました。物理学の世界では、ブラックホールは「毛がない」と言われます。どんな複雑な情報を持つ物質を飲み込んでも、最終的にブラックホールを特徴づける性質が「質量」「角運動量（自転）」「電荷」の3つだけになってしまう、という「ノーヘア・セオリー」です。これはブラックホールが、飲み込んだもののエントロピーを消し去ってしまう、超・秩序的な天体であることを示唆し、物理学者たちを長年悩ませました。

この大問題を解決したのが、物理学者ジェイコブ・ベッケンシュタインとスティーヴン・ホーキングでした。彼らは、革命的な結論に達します。

これは、部屋の散らかり具合（エントロピー）が、部屋の広さ（体積）ではなく、壁紙の総面積だけで決まってしまう、と宣言するようなものです。この理論によれば、ブラックホールはとてつもなく巨大なエントロピーを持っています。エントロピーを消し去る存在どころか、むしろ宇宙に存在するあらゆるものの中で、最も効率的にエントロピーを溜め込む「怪物」だったのです。

新たな戦場：「ブラックホール情報パラドックス」

しかし、話はここで終わりません。ホーキングは、ブラックホールが「ホーキング放射」によって非常に長い時間をかけて蒸発し、消滅することを発見します。この発見は、物理学史上最も深刻な謎の一つを生み出しました。それが「ブラックホール情報パラドックス」です。

このパラドックスは、私のような宇宙好きにとって、物理学の最もエキサイティングな最前線です。そこでは、現代物理学の二大巨頭が、互いに譲らず睨み合っています。

1. 量子力学の大原則: 「情報は絶対に失われない（ユニタリ性）」と定める。これは、過去から未来へ情報が繋がるための根幹です。
2. ブラックホールの蒸発: しかし、ブラックホールが完全に蒸発して消滅するなら、飲み込まれた物質が持っていた情報（それが「百科事典」だったのか「リンゴ」だったのか）は、一体どこへ行ってしまうのか？
3. 物理学の危機: もし情報が本当に消滅するなら、過去から未来へと繋がる因果律の根幹が揺らぎ、物理学の土台が崩壊してしまう。

物理学者たちは今、この難問を解くために壮絶な知の格闘を繰り広げています。情報は、熱放射の中に難解な形でエンコードされて外に出るのか？あるいは「ホログラフィック原理」（宇宙のすべての情報は、その境界の表面に記録されているという驚くべきアイデア）が示すように、情報はそもそも3次元の内部ではなく、2次元の事象の地平面に記録されているのか？この謎の答えの先にこそ、次の物理学革命の扉が待っているのです。

ブラックホールすらも、この壮大な法則の前では永遠ではいられません。では、最後に残された私たち自身の宇宙を待ち受ける運命とは？ 最後の章では、エントロピーが増大しきった宇宙の、静かなる果てを旅します。

第4章：宇宙の終焉シナリオ – 静寂の未来「熱的死」は絶対か？

エントロピー増大の法則が描き出す、宇宙の究極的な未来。それが「熱的死（Heat Death）」です。これは、宇宙の膨張が永遠に続いた場合に訪れる、エントロピーが最大に達した静寂の世界を指します。

もちろん、宇宙の終焉には他にもいくつかのシナリオが考えられています。宇宙が膨張から収縮に転じる「ビッグクランチ」や、加速膨張が無限に続き、原子さえも引き裂かれる「ビッグリップ」などです。しかし、現在の観測でダークエネルギーによる宇宙の加速膨張が示唆されている以上、この「熱的死」が最も有力な未来だと考えられています。

熱的死に至るまでの道のりは、私たちの想像を絶する、あまりにも長大な叙事詩です。この時間を思う時、私はいつも畏敬の念に打たれます。

1. 星々の時代の終わり（約100兆年後、$10^{14}$年後）:
   宇宙に存在する全ての恒星が燃え尽き、宇宙は光を失います。残されるのは、白色矮星、中性子星、そしてブラックホールだけです。
2. 物質の消滅（約$10^{36}$年後以降）:
   大統一理論が予測するように「陽子崩壊」が起こるなら、星々の残骸や惑星といった物質そのものが崩壊し、光子や素粒子となって宇宙を漂います。
3. ブラックホールの蒸発（最大で約$10^{100}$年後）:
   最後に残ったブラックホールも、ホーキング放射によって気の遠くなるような時間をかけて蒸発します。「1の後に0が100個も続く」年数をかけて、最後の一滴までエネルギーを宇宙に返します。

最終的に宇宙は、絶対零度に限りなく近い温度で、エネルギーの低い光子や素粒子がまばらに漂う、完全な静寂と均一の世界に達します。エネルギーの「勾配」が失われ、流れが完全に停止し、いかなる活動も、いかなる計算も、いかなる生命も起こりえない。

それが、エントロピーが増大しきった宇宙の最終形態、「熱的死」です。

まとめ：宇宙の流れの中で、束の間の奇跡を生きる私たち

ここまで、部屋の散らかりから宇宙の終焉まで、壮大なエントロピーの旅をしてきました。

コーヒーにミルクが混ざるのも、時間が過去に戻らないのも、そして宇宙がいつか完全な静寂を迎えるのも、すべては「物事は、より確率の高い（場合の数が多い）状態へと移行する」という、驚くほどシンプルで強力な一本の線で繋がっています。

この法則の探求は、私にとって、単に物理の知識を得ること以上の意味がありました。それは、なぜ世界が一方通行で、不可逆的なのか、その根源的な理由に触れることです。そして、エントロピー増大という絶対的な流れの中に、生命や知性といった「秩序」が、いかに奇跡的で、儚く、そして尊いものであるかを教えてくれます。

だから、次にあなたの部屋が散らかった時、少しだけ宇宙のことを思ってみてください。それは単なる怠惰の結果ではなく、あなたがこの宇宙の根源的な法則の一部である証なのです。そして、その流れの中で、私たちが何かを学び、創造し、愛するということ。その秩序ある活動こそが、束の間の、しかし何よりも美しい奇跡なのです。

参考文献