はじめに:なぜ400年前の法則が、現代宇宙論の最前線で輝くのか?
もし、宇宙に浮かぶ星々の重さを測ることができる「天秤」があるとしたら、信じられますか?
今から400年以上も前、一人の天文学者が発見したシンプルな法則が、まさにその「宇宙の天秤」として機能しています。その名は「ケプラーの第3法則」。
この法則は、一見すると惑星の動きを記述しただけの古典的なものに見えるかもしれません。しかしその本質は、遠い恒星の周りを回る未知の惑星(系外惑星)の正体を暴き、銀河に潜む謎の物質「ダークマター」の存在を示唆し、さらには私たちの生活に欠かせないGPS衛星の軌道を支える、現代宇宙物理学の根幹をなす強力なツールなのです。
この記事では、ケプラーの第3法則が発見されるまでの苦難の物語から、その数式が持つ真の意味、そして現代の宇宙研究でどのように使われているのかまで、壮大な旅にご案内します。この旅を終える頃には、夜空の星々が、単なる光の点ではなく、物理法則が奏でる壮大なシンフォニーとして見えてくるはずです。
この記事でわかること
- 法則発見の物語: 天才ティコ・ブラーエと不屈のケプラーが織りなす、歴史的な発見の裏側
- 数式の本質: 「周期の2乗が距離の3乗に比例する」というシンプルな法則が持つ、驚くべき意味
- 物理学的な意味: ニュートンが解き明かした「なぜ」と、宇宙の質量を測る方程式への進化
- 現代への応用: 系外惑星探査からダークマターの謎まで、最前線の宇宙研究との繋がり
第1章:ティコ・ブラーエの観測とケプラーの執念が生んだ「調和の法則」
ケプラーの法則は、一人の天才の頭脳から閃きのように生まれたわけではありません。そこには、師であるティコ・ブラーエの生涯をかけた観測と、ケプラー自身の執念ともいえる探求の物語がありました。
16世紀末、デンマークの天文学者ティコ・ブラーエは、望遠鏡がない時代に、肉眼での天体観測の精度を極限まで高めた人物でした。彼は巨大な観測装置を自作し、何十年にもわたって惑星、特に火星の位置を驚異的な精度で記録し続けます。
一方、数学に秀でたドイツの天文学者ヨハネス・ケプラーは、宇宙は神が創造した調和のとれた世界であり、その動きは美しい幾何学で説明できるはずだと信じていました。運命に導かれるようにティコの後継者となったケプラーは、師が遺した膨大な火星の観測データを引き継ぎ、その軌道の謎に挑みます。
当初、ケプラーは「惑星の軌道は完璧な円である」という、古代ギリシャから続く信念に基づいて計算を進めました。しかし、彼の計算結果は、ティコの精密なデータとどうしてもわずか8分角(満月の見かけの直径の約1/4)だけズレてしまうのです。
他の者なら無視したかもしれない、このあまりに小さな誤差。しかし、師の観測精度を信じるケプラーは、このズレを「神が与えた真実へのヒント」だと考え、円軌道という長年の常識を捨てるという、あまりに大胆な決断を下します。この姿勢は、後の科学革命にも繋がる重要な一歩でした。
そして数えきれないほどの試行錯誤の末、彼はついに真実にたどり着きます。惑星は円ではなく「楕円」を描いて運動していたのです(ケプラーの第1法則)。さらに、惑星は太陽に近いほど速く、遠いほど遅く動くことも発見しました(第2法則)。
第1、第2法則の発見から約10年。ケプラーは探求を止めませんでした。彼は、各惑星の「公転周期」と「太陽からの距離」の間に、何か関係があるはずだと信じて計算を続けます。そして1618年、ついに宇宙の壮大なハーモニーを数式で表現することに成功します。
それが「惑星の公転周期の2乗は、軌道の大きさ(長半径)の3乗に比例する」というケプラーの第3法則、彼自身が「調和の法則」と呼んだ発見でした。このシンプルな法則が持つ意味を、次の章で詳しく見ていきましょう。
第2章:数式で理解するケプラーの第3法則 – 惑星たちの完璧なシンフォニー
ケプラーが見つけた「調和の法則」は、数式で書くと非常にシンプルです。
P² ∝ a³
これは「Pの2乗はaの3乗に比例する」と読みます。ここで、
- P (Period) は、惑星が太陽の周りを一周するのにかかる時間、つまり公転周期です。
- a (axis) は、惑星の楕円軌道の「長半径」、つまり太陽からの平均的な距離と考えてください。
この法則が意味するのは、太陽系のすべての惑星が、このシンプルな数式という一つのルールに従って動いているということです。太陽から遠い惑星ほど、公転周期(P)が劇的に長くなる関係性を見事に示しています。
言葉だけではピンとこないかもしれません。実際に太陽系の惑星たちのデータを見てみましょう。比較しやすいように、地球を基準(1)とします。
| 天体 | 軌道長半径(a) [地球=1] | 公転周期(P) [地球=1年] | P² (周期の2乗) | a³ (距離の3乗) |
|---|---|---|---|---|
| 水星 | 0.39 | 0.24 | 0.06 | 0.06 |
| 金星 | 0.72 | 0.62 | 0.38 | 0.37 |
| 地球 | 1.00 | 1.00 | 1.00 | 1.00 |
| 火星 | 1.52 | 1.88 | 3.53 | 3.51 |
| 木星 | 5.20 | 11.86 | 140.7 | 140.6 |
| 土星 | 9.58 | 29.45 | 867.3 | 879.2 |
ご覧ください。どの惑星も「P²」と「a³」の値が、驚くほどよく一致しているのがわかります。ケプラーは、惑星たちが奏でる宇宙の音楽の「楽譜」を発見したのです。
この驚くほど正確な惑星たちのハーモニー。しかし、その美しい音楽を指揮している「指揮者」の正体、すなわち「なぜ」惑星はそのように動くのか、その根本原因はまだ誰も知りませんでした。その謎を解き明かす一人の天才が、イギリスに現れるのです。
第3章:ニュートンの万有引力が解き明かした「なぜ」 – 宇宙の質量を測る方程式へ
「惑星はなぜ、ケプラーが発見した法則通りに動くのだろう?」
ケプラーの法則は、惑星の動き(HOW)を完璧に描き出しました。しかし、その動きを引き起こす根本的な原因(WHY)については、彼自身も説明することができませんでした。その長年の謎に、物理的な答えを与えたのが、かの有名なアイザック・ニュートンです。
結論から言うと、ニュートンは「万有引力」という自然界の根本的な力によって、ケプラーの3つの法則すべてを数学的に証明してみせました。 これにより、ケプラーの法則は単なる観測結果のまとめから、宇宙の質量さえも測れる、物理学の強力な方程式へと進化したのです。
天上と地上のルールを統一した「万有引力の法則」
ニュートンが登場するまで、空で起こる天体の運動と、地上でリンゴが木から落ちるような運動は、まったく別のルールで支配されていると考えるのが一般的でした。
しかし、ニュートンは違いました。彼は「すべての質量を持つ物体は、互いに引き合う力(引力)を及し合っている」という、とてつもなく普遍的なアイデアを提唱します。これが万有引力の法則です。
この法則のすごいところは、惑星を軌道につなぎとめている力も、地面にリンゴを引き寄せる力も、本質的にはまったく同じ「引力」であると見抜いた点にあります。この発見によって、天の世界も地の世界も、同じ一つの物理法則で語れるようになりました。
方程式へ進化:宇宙の質量を測る「天秤」の誕生
ニュートンは、自らが体系化した運動の法則と万有引力の法則を組み合わせることで、ケプラーが見つけた惑星の運動法則を、すべて数学の言葉で導き出すことに成功しました。
彼が導き出した、より精密なケプラーの第3法則の姿がこちらです。
P² = (4π² / G(M+m))a³
新しい記号 `G` は万有引力定数と呼ばれます。これは、質量がどれくらいの強さで引力を生み出すかを決める、いわば「宇宙の重力換算レート」のようなものです。
この式の発見が、天文学に革命をもたらしました。なぜなら、この式を M について解けば、中心天体の質量を計算できるからです。
ここで、多くの方がつまずきやすいポイントがあります。「計算するには、地球の質量(m)も必要じゃないか?」と。その通りです。しかし、太陽の質量(M)は地球の質量(m)の約33万倍もあります。Mにmを足しても、その合計値はほとんど変わりません。
そのため、この式は実用上、以下のように近似できます。
P² ≈ (4π² / GM)a³
この式の意味するところは、まさに「宇宙の天秤」です。私たちが知りたい太陽の質量(M)は、地球の公転周期(P:約365日)と、太陽と地球の平均距離(a:約1億5000万km)を観測するだけで、計算できてしまうのです。
第4章:現代天文学の最前線 – 系外惑星からダークマターまで
ニュートンによって物理学的な裏付けを得たケプラーの第3法則は、400年の時を超え、現代天文学の最前線で目覚ましい活躍を見せています。
1. 未知の惑星の重さを測る(系外惑星探査)
近年、数千もの太陽系外惑星が発見されていますが、その多くは恒星の前を惑星が横切る際のわずかな光の変化(トランジット)を捉えることで見つかります。このトランジット法により、惑星の公転周期(P)を知ることができます。
しかし、周期だけでは惑星が巨大なガス惑星なのか、生命が宿るかもしれない岩石惑星なのかは分かりません。そこで活躍するのがケプラーの第3法則です。恒星の質量(M)が分かっていれば、公転周期(P)から惑星までの距離(a)を計算できます。最終的に惑星の質量(m)を推定できるのです。
2. 見えない”何か”の存在を暴く(ダークマター)
ケプラーの法則は、目に見える天体だけでなく、目に見えないものの存在を暴き出すことさえあります。その代表例がダークマターです。
銀河内の星々の回転速度は、私たちが観測できる物質の質量だけから計算される予測よりも、遥かに速いのです。この矛盾は、「光では観測できないが、重力だけは及ぼす未知の質量が、銀河全体を包み込んでいる」と考えると説明できます。
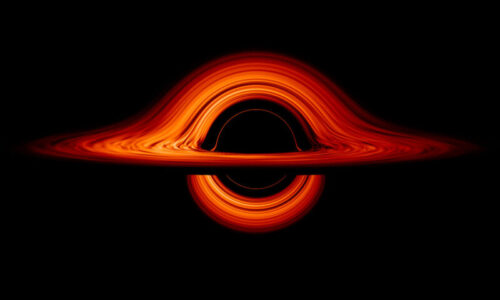
3. 超巨大ブラックホールの正体に迫る
私たちの天の川銀河の中心には、太陽の400万倍もの質量を持つ超大質量ブラックホールが存在すると考えられています。その質量は、周りを猛スピードで公転する星々の公転周期(P)と軌道(a)を精密に測定し、ケプラーの第3法則に当てはめることで正確に算出されました。
まとめ:古典法則から、宇宙の謎に挑む普遍的なツールへ
ティコ・ブラーエの眼と、ケプラーの不屈の精神から生まれた「調和の法則」。それは、ニュートンの手によって「万有引力」という物理的な意味を与えられ、宇宙の質量を測る「天秤」へと進化しました。
そして現代、その天秤は、私たちが見たこともない系外惑星の重さを測り、宇宙の95%を占めるとされるダークマターやダークエネルギーの謎に迫り、銀河の中心に潜むブラックホールの正体を暴くための、最も信頼できる道具の一つとして、今なお輝き続けています。
400年以上も前に発見された一つの法則が、人類の宇宙観を塗り替え、未知への扉を開き続けている。この事実こそ、科学の探求が持つ面白さと、普遍的な法則の美しさを、何よりも雄弁に物語っているのではないでしょうか。